By Will Young, Solution Architect, UnderwriteMe

How do you keep a secret?

That’s an important question at UnderwriteMe. We send gigabytes of data over the internet every day. Almost all of this is sensitive data that we don’t want anyone to be able to read. It’s not just personal data, but often people’s medical records. If we don’t convert the data into something unreadable – called encrypting – before sending it, anyone would be able to see what we’re sending as it goes across the Internet. Once the encrypted data has been sent, the recipient also needs a way to decrypt it, or convert the message back into readable data.

People have always kept secrets. In Roman times, each letter would be substituted by a letter further down the alphabet. A would become D, B would become E, and XYZ would become ABC. This approach has limitations. Only 26 shifts are possible, and you just need to try each before you can decode it.

Another approach would be to randomly replace each letter. The letter A would be replaced with R, B might become W, S or any other letter. This increases the search space. There are now about 403,291,460,000,000,000,000,000,000 potential shifts. It’s now much harder for a human to crack the code, but with a computer we can break these substitution-bases reasonably quickly. In fact, that’s what the Enigma machine did during the war. But it still leaves a problem. How do you tell someone what the key – in this case which letters are substituted for which – is, without telling everyone what the key is?

The chicken-and-egg problem of how to send a secret message without sending a key first went unsolved for centuries. Like busses, then two solutions came at the same time.

In 1969 Clifford Cocks was working at GCHQ, the UK spying agency. He found a way to send a message without sending a key*. Rather than a single key that both encrypted and decrypted, his method used two keys, one that encrypted, and one that decrypted.

The key that encrypted could be handed out freely, because it could only take some information and make a copy that only you could decrypt. Because it could be made available to anyone, it was called the public key. The key that was used to decrypt the secret message had to be kept a secret and wasn’t sent to anyone. This is the private key.

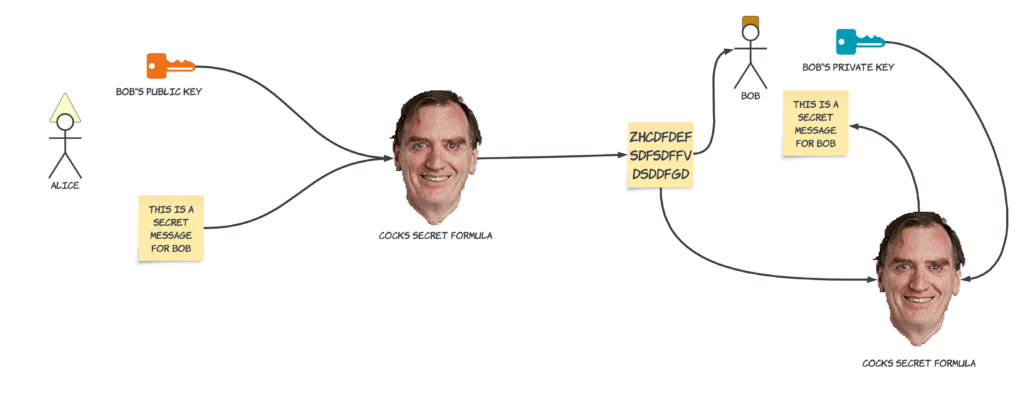
When you used Cocks’s formula, you take a number – or some text encoded as numbers – along with the public key and produce the encrypted version. If you ran it again, this time using the private key, the original text would come out the other side.

In the diagram below, Alice (on the left) is sending a message to Bob. She takes Bob’s public key and her message and feeds it into Cocks’s Secret Formula. This produces the encrypted version of her message, “ZHCDFDEFDFSDFFVDSDDFGD”. Bob takes the encrypted version and feeds it back into Cocks’s formula along with his private key, and the original message comes out.

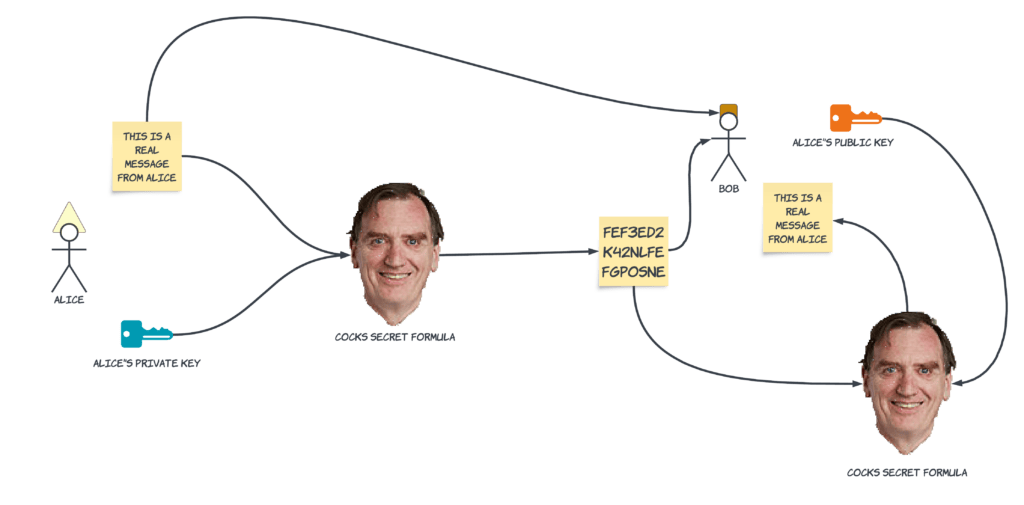
The formula is useful both ways. I can run it with a bit of text and the public key to create a secret. But if I run it through with the text and a private key, I get something useful as well. Anyone can now use the public key to decrypt the text, but since only the private key could have created that string, it provides a means of signing, or proving the authenticity of some text. As long as the private key remains private, I can keep secrets and provide proof to others that some text wasn’t faked.

In the diagram below, Alice is again sending a message to Bob, but this time her concern is that Bob won’t be able to know that it’s really from her, and not a forgery. She generates a signature using her private key, and sends that, along with the message, to Bob. Bob takes the signature and runs it through Cocks’s formula again, along with the public key. He can compare the output with the original message, and he knows that it was from Alice.

Cocks’s invention relied on some unique mathematical properties relating to prime numbers (those numbers that are only divisible by 1 and themselves, like 17, 31, 43, and 8191^** and what the remainder is when you divide a large number. The keys themselves are just very large numbers. There are two large numbers in the public key, one of which – we’ll call it n – is a number that’s the result of multiplying two very large prime numbers. It’s important that the numbers are really large, because in order to figure out what the private key is when you only know the public key, you have to figure out what two prime numbers can be multiplied together to get n.

For example, if n is 35, most people could figure out pretty quickly that those two primes are 5 and 7. So any numbers we use will need to be pretty big. For encryption, “pretty big” is somewhat understating things. A typical key will be 2048 bits long. That’s a number 617 digits long. By comparison, the number of atoms in the universe is about 80 digits long. Humans don’t really process numbers that large, so if a hacker wanted to figure out your private key, they’d need to use a computer.

As it turns out, that’s really hard, even for a computer. You can’t directly calculate what the numbers are, you have to guess and check. With the most advanced algorithms, the time required to do this is proportional to the square root of the number of digits^***. This could be calculated, but it would take years.

Quantum computers, which take advantage of physical phenomena very different to those used in normal computers would be able to do the calculation much more quickly but aren’t currently practical to build. It’s been over 40 years since the first quantum computers and algorithms, or formulas, were proposed, so this seems unlikely to change anytime soon.

If computational power doubles every 18 months, as is has for decades, it might be possible to crack the key if it were valid indefinitely. This is why any key comes with a fixed validity. It might be a secret for now, but a determined attacker could calculate your private key if they had 5 or 10 years to do so.

This is also why we have to update certificates. Under the hood, each certificate has public and a private key. We change these out to make sure that an attacker will never be able to impersonate us, or our clients, that client communications are protected, and that only the right people have access to things.

It’s quite the achievement for Cocks. Unfortunately for him, his work was classified and GCHQ didn’t think it was practical. Nobody would know about it until 1997 when the papers we released.

The use of separate keys was later proposed by Ralph Merkle, Whitfield Diffie, and Martin Helman, unaware of the work at GCHQ. The key exchange that happens today is named after Diffie and Helman, who were able to publish unencumbered by the Official Secrets Act.

4 years after his work, 3 mathematicians at MIT, Ron Rivest, Adi Shamir and Leonard Adleman independently discovered his formula. They patented it and started a company, RSA, to monetise their discovery. That company was sold for $1.5 billion in 2006.

The same basic technique is still used today to keep our data – and clients’ data – a secret. It’s not just us. Every time you enter a credit card number on a retail site or any other secure connection, you’re using Clifford Cocks’s secret formula. He didn’t become a billionaire, but he still gets the bragging rights.

^*Two other mathematicians, James Ellis and Nick Patterson also contributed ideas, especially around the use of separate keys.

^**8191 is an example of a Mersenne Prime, but let’s not get too crazy for this

*** for the pedants, L_n[1/2,1] or O(e^{(ln ln n)^1/2})

Image credit By Royal Society uploader – Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=43268163